登录/ 注册
 找回密码
 立即注册
关闭

CSDN热搜

程序园 精品问答 技术交流 资源下载
返回列表 发新帖
首页 › 业界区 › 业界 ›树与二叉树

树与二叉树

瘴锲如 2025-6-3 10:40:44
github仓库：https://github.com/EanoJiang/Data-structures-and-algorithms
树

定义

1.png

结点的度数其实就是这个结点下连的线，比如：A的度 = AB+AC+AD = 3
树的度就是MAX(结点的度)
叶子结点就是没后代的结点
树的基本性质


  • 所有结点数 = 所有结点的度数之和 + 1(这个1也就是根节点)
    习题：
    2.png

    所有节点数 =4 + 20 * 4 + 10 * 3 + 1 * 2 + 10 * 1  +  1  = 123
    123 - 20 - 10 - 1 - 10 = 82
  • 所有结点数 =  不同度的节点数 之和
    假设所有节点数为n，度0～4的个数为n0～n4，则n = n0 + n1 + n2 + n3 + n4
  • 3.png

    第一层m0，第二层m1，第i层m^(i-1)
  • 4.png

    等比数列求和公式
二叉树

定义

5.png

就是每个分支只有二叉的树，子树有左右之分
基本形态

6.png

二叉树的性质


  • 7.png

    这是某一层的最多结点数
  • 8.png



  • 这是整个二叉树的最多结点数

  • n0 = n2 + 1
    对于任何非空的二叉树，度0(叶子)和度2的结点数为n0、n2，那么 n0 = n2 + 1
    n2 = 0 的时候，n0 = 1，每把一个叶子画一个二叉，n2++，n0++
    n = 1 * n1 + 2 * n2 + 1
    n = n0 + n1 + n2
    解得，n0 = n2 + 1

特殊二叉树

满二叉树

9.png

完全二叉树

10.png

没有左子树，不能有右子树，上一层没铺满，不能有下一层
判断完全二叉树
11.png

不是
12.png

是
完全二叉树的性质

1.2.3.就是二叉树的性质

  • 13.png

  • 14.png

  • 如果总结点数-1是奇数，说明有一个度为1的结点
习题
15.png

叶子结点出现在最后2层，这里求的是最多，所以最后一层是第7层
第6层最多的结点数=2^(6-1)=32
第6层的非叶子结点=32-8=24
第7层的最多结点数= 24*2 = 48
前6层的最多结点数=2^6 - 1 = 63
总计=63+48 = 111，选c
16.png

n = n0+n1+n2
n0=n2+1
所以，n = 2n2 + n1 + 1
而768-1是奇数，所以有一个度为1的结点，即n1 = 1
解得 n2 = 383
n0 = n2 + 1 = 384，选c
17.png

n=n0+n1+n2
n1 = 0
n0=n2+1
所以，n = 2n0 - 1 = 2k -1 ，选a
二叉树的实现

顺序结构实现——除了满二叉树和完全二叉树的其他场景比较浪费空间
链式结构实现

18.png
  1. //链式结构实现
  2. typedef char ElemType;
  4. //树结点
  5. typedef struct TreeNode {
  6.     ElemType data;
  7.     TreeNode *lchild;
  8.     TreeNode *rchild;
  9. } TreeNode;
  11. //用树结点指针表示二叉树
  12. typedef TreeNode* BiTree;
复制代码
创建二叉树

二级指针概念：
19.png

指针pp 存的是 指针p的地址
那么*pp 就是 得到p的地址，**pp就是得到p的值
  1. char str[] = "ABDH#K###E##CFI###G#J##";
  2. int idx = 0;
  4. //创建二叉树
  5. // T是二级指针(BiTree**)
  6. //  *T就是对二叉树的结点进行操作
  7. void createTree(BiTree *T)
  8. {
  9.         ElemType ch;
  10.         ch = str[idx++];
  11.         if (ch == '#')
  12.         {
  13.                 *T = NULL;
  14.         }
  15.         else
  16.         {
  17.                 *T = (BiTree)malloc(sizeof(TreeNode));
  18.                 (*T)->data = ch;
  19.                 createTree(& ( (*T)->lchild ) );
  20.                 createTree(& ( (*T)->rchild ) );
  21.         }
  22. }
复制代码
遍历

前序遍历

NLR / NRL （根-左-右）/（根-右-左）
不特别说明，一般情况都是先左的遍历
从根节点开始，先从左子结点开始一层层向下递(进栈)并打印，如果左子节点是空就归(出栈)，然后开始递右结点，进行如上同样操作，并向上一层层归，归到根节点后，对根节点的右子节点进行同样的操作。
具体动画演示可以看《数据结构（C 语言描述）》的55:00左右进度条
  1. //前序遍历
  2. void preOrder(BiTree T){
  3.     if(T == NULL) return;
  4.     printf("%c ", T->data);
  5.     //递归子树
  6.     preOrder(T->lchild);
  7.     preOrder(T->rchild);
  8. }
复制代码
中序遍历

LNR / RNL
从根节点开始，先从左子结点开始一层层向下递(进栈)，如果左子节点是空就归(出栈)并打印，然后开始递右结点，进行如上同样操作，并向上一层层归，归到根节点后，对根节点的右子节点进行同样的操作。
  1. //中序遍历
  2. void inOrder(BiTree T){
  3.     if(T == NULL) return;
  4.     inOrder(T->lchild);
  5.     printf("%c ", T->data);
  6.     inOrder(T->rchild);
  7. }
复制代码
后序遍历

LRN / RLN
从根节点开始，先从左子结点开始一层层向下递(进栈)，如果左子节点是空就归(出栈)，然后开始递右结点，进行如上同样操作，在右结点空的时候归(出栈)并打印，并向上一层层归，归到根节点后，对根节点的右子节点进行同样的操作。
  1. //后序遍历
  2. void postOrder(BiTree T){
  3.     if(T == NULL) return;
  4.     postOrder(T->lchild);
  5.     postOrder(T->rchild);
  6.     printf("%c ", T->data);
  7. }
复制代码
习题
20.png

前：ABDHEICFGJK
中：HDBEIAFCJGK
后：HDIEBFJKGCA
21.png

前：ABDEGHCFI
中：DBGEHAFIC
后：DGHEBIFCA
22.png

先画出二叉树：
  1.          A
  2.         / \
  3.        B   D
  4.       /   / \  
  5.      C   E   F
复制代码
后：CBEFDA
二叉树遍历性质

23.png

习题
24.png

先右后左的中序遍历，RNL，选d
25.png

26.png

ADB都能画出来，所以选c
27.png
  1.         1
  2.          \
  3.           2
  4.            \
  5.             3
复制代码
选b
(这题不要多选，一般情况只需要考虑先左就行)
28.png
  1.          f
  2.        /   \
  3.       c     g
  4.        \   /
  5.         a d
  6.        /   \
  7.       e     b
复制代码
选b
29.png

因为对于顺序结构来说，没有的子树节点需要填NULL，所以相当于是高度为5的满二叉树需要的存储单元，也就是二叉树的最大结点数公式，即2^5 - 1 = 31
线索二叉树

30.png

目标：构建一个双向循环链表
31.png

会出现空余空间不够用的情况吗？
不会，n个节点有n+1个空
代码实现

32.png
  1. typedef char ElemType;
  3. typedef struct ThreadNode {
  4.     ElemType data;
  5.     struct ThreadNode *lchild, *rchild;
  6.     int ltag, rtag;
  7. } ThreadNode;
  9. typedef ThreadNode *ThreadTree;
复制代码
ltag：0 指向lchild，1指向前驱
rtag：0 指向rchild，1指向后继
中序遍历线索化

33.png
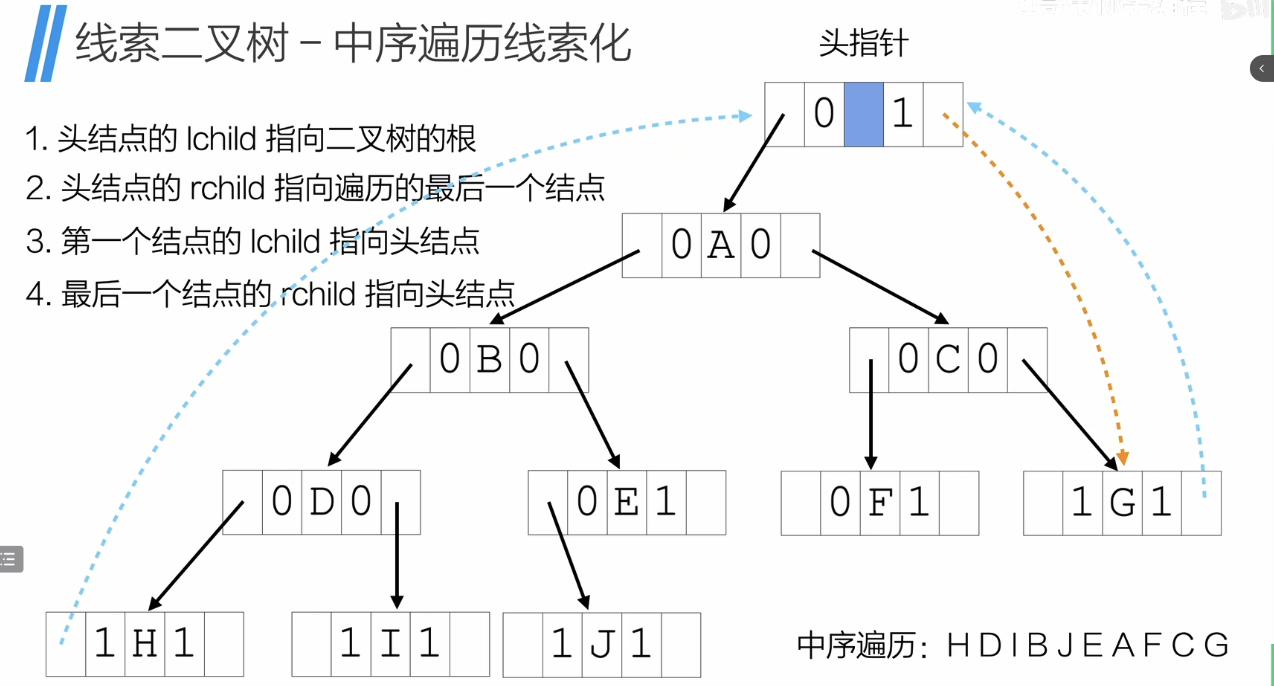
  1. #include #include typedef char ElemType;
  3. typedef struct ThreadNode {
  4.     ElemType data;
  5.     struct ThreadNode *lchild, *rchild;
  6.     int ltag, rtag;
  7. } ThreadNode;
  9. typedef ThreadNode *ThreadTree;char str[] = "ABDH##I##EJ###CF##G##";int idx = 0;ThreadTree prev;//创建二叉树void createTree(ThreadTree *T){    ElemType ch;        ch = str[idx++];        if (ch == '#')        {                *T = NULL;        }        else        {                *T = (ThreadTree)malloc(sizeof(ThreadNode));                (*T)->data = ch;                createTree(& ( (*T)->lchild ) );        //lchild有左孩子，则ltag=0        if( (*T)->lchild != NULL){            (*T)->ltag = 0;        }        createTree(& ( (*T)->rchild ) );        if( (*T)->rchild != NULL){            (*T)->rtag = 0;        }        }}//线索化——加前驱后继的逻辑void threading(ThreadTree T){    if(T != NULL){        //一直往左边遍历        threading(T->lchild);        //当前结点的左孩子为空，当前结点的左孩子设定为指向前驱        if(T->lchild == NULL){            T->ltag = 1;            T->lchild = prev;        }        //前驱结点的右孩子为空，前驱结点的右孩子设定为指向当前结点(当前结点就是前驱节点的后继)        if(prev->rchild == NULL){            prev->rtag = 1;            prev->rchild = T;        }        //更新prev到根节点，往右边遍历        prev = T;        threading(T->rchild);    }}//中序遍历线索化void inOrderThreading(ThreadTree *head ,ThreadTree T){    *head = (ThreadTree)malloc(sizeof(ThreadNode));    (*head)->ltag = 0;    (*head)->rtag = 1;    (*head)->rchild = (*head);    if(T == NULL){        (*head)->lchild = (*head);    }    else{        //头节点的左孩子指向树的根节点        (*head)->lchild = T;        //prev：上一个访问的节点是头节点        prev = (*head);        //加前驱后继的逻辑        threading(T);        //最后一个节点的右孩子指向头节点        prev->rtag = 1;        prev->rchild = (*head);        //头节点的右孩子指向遍历的最后一个节点        (*head)->rchild = prev;    }}//基于线索的中序遍历void inOrder(ThreadTree T){    ThreadTree current = T->lchild;    while(current != T){        //如果当前节点有左孩子，则一直往左边遍历        //没有左孩子，则退出当前循环 输出当前节点        while(current->ltag == 0){            current = current->lchild;        }        printf("%c",current->data);        //往右边遍历, 直到右孩子不为空且当前的右孩子是头节点        while(current->rtag == 1 && current->rchild != T){            current = current->rchild;            printf("%c",current->data);        }        current = current->rchild;    }    printf("\n");}int main(){    ThreadTree head;    ThreadTree T;    createTree(&T);    inOrderThreading(&head,T);    inOrder(head);    return 0;}
复制代码
习题
34.png

后序遍历：dbca
左虚线是前驱，右虚线是后继
根节点的前驱是头节点NULL
选D
35.png
  1.         根节点
  2.          / \
  3.         Y   X
复制代码
后序遍历：YX根
右虚线是后继，所以X的右线索指向根，也就是父节点
选A
36.png

中序遍历：debxac
左虚线是前驱，右虚线是后继
所以b、a
选D
哈夫曼树

为什么要学哈夫曼树？
37.png

对于这样一个问题，通常用if分支表示
38.png

效率很低啊，有没有效率高的方式呢？

有的兄弟有的
来源：程序园用户自行投稿发布，如果侵权，请联系站长删除
免责声明：如果侵犯了您的权益，请联系站长，我们会及时删除侵权内容，谢谢合作！

使用道具 举报
B Color Image Link Quote Code Smilies
您需要登录后才可以回帖 登录 | 立即注册
发帖
瘴锲如
2025-6-3 10:40:44

0

粉丝关注

11

主题发布

板块介绍填写区域，请于后台编辑
微信扫一扫