B站学习的视频链接 用pytorch实现线性回归
目录
- 1 复习引入
- 2 模型建立
- 1 训练数据
- 2 设计模型
- 3 构造损失函数和优化器
- 4 做好训练的过程
- 3 代码综合
- 总结
- 1 深度学习的流程
- 2. 代码处理
- 3 函数总结
- torch.tensor()
- torch.nn.Linear()
- torch.nn.MSELoss()
- torch.optim.SGD()
- .zero_grad()
- .backward()
- Model.linear.weight.item()
- Model.linear.bias.item()
1 复习引入
和上一次一样采用的是这个比较基本的模型进行讲解,并且采用随机下降模型梯度
在上一讲中已经使用了一定的pytorch的模型
- tensor:数据
- backward()自动反馈求解处理。
2 模型建立
1 训练数据
给定一定的样本数据
这次咱们应当使用的是具体的pytorch的数据结构进行输入,采用的是\(mini\ batch\)。
也就是说将\(x\)和\(y\)放在一起即可。
例如:\((x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})\)- import torch
- x_data = torch.Tensor([[1.0], [2.0], [3.0]])
- y_data = torch.Tensor([[2.0], [4.0], [6.0]])
注意:x和y必须是矩阵。
2 设计模型
用来计算咱们的\(\hat{y}\)
根据比较基本的模型也就是线性模型而言:\(\hat{y}=w\times x + b\)
如果输入的数据是上面那个样子的话,那么咱们的\(\hat{y}\)就可以变成,\(\begin{cases}\hat{y}_{1}=w\cdot x_{1}+b\\\hat{y}_{2}=w\cdot x_{2}+b\\\hat{y}_{3}=w\cdot x_{3}+b&\end{cases}\)
这个时候就可以采用向量的写法了:\(\left.\left[\begin{array}{c}{\hat{y}_{1}}\\{\hat{y}_{2}}\\{\hat{y}_{3}}\end{array}\right.\right]=w\cdot\begin{bmatrix}{x_{1}}\\{x_{2}}\\{x_{3}}\end{bmatrix}+b\)
之前咱们是人工求导数的,现在咱们最重要的事情是构造计算图,求导是\(pytorch\)的事情。
这个时需要要确定权重的性转和\(b\)的大小。
如果想要知道权重的形状那么就需要知道输入的一个维度形状。
注意输出的\(loss\)必须是一个标量。
在pytorch中首先先将模型定义成一个类。
每一个类一定要继承咱们的Module模块
注意:必须要这两个函数,一个是__init__()另一个是forward()名字都不可以错。
- class LinearModel(torch.nn.Module):
- def __init__(self):
- super(LinearModel, self).__init__() # 调用副类,直接这么写就完了。
- self.linear = torch.nn.Linear(1, 1) #nn.linear()是pytorch的一个类,这两个分别是权重和偏置。也在构造一个对象。 Neural network nn.Linear(输入维度,输出维度)。
- def forward(self, x): # forward的函数名是固定的。
- y_pred = self.linear(x) #实现了一个可以调用的对象。
- return y_pred
- model = LinearModel() # 实例化
nn.Linear(in_features,out_features,bias=True)
- in_features : size of each input sample
- out_features : size of each output sample
- bias : If set to False, the layer will not learn an additive bias. Default: True
- class LinearModel(torch.nn.Module):
- def __init__(self):
- super(LinearModel, self).__init__()
- self.linear = torch.nn.Linear(1, 1)
- def forward(self, x):
- y_pred = self.linear(x)
- return y_pred
- model = LinearModel()
使用pytorch的应用接口进行构造。
咱们原本的模型为:\(loss = (\hat{y}-y)^2\)
那么对于这么一堆数据就有:\(loss_{1}=(\hat{y}_{1}-y_{1})^{2} \\loss_{2}=(\hat{y}_{2}-y_{2})^{2} \\loss_{3}=(\hat{y}_{3}-y_{3})^{2}\)。
这时候用向量的形式可以表示为:\(\begin{bmatrix}\log_2\\\log_2\\\log_3\end{bmatrix}=\begin{pmatrix}\begin{bmatrix}\hat{y}_1\\\hat{y}_2\\\hat{y}_3\end{bmatrix}-\begin{bmatrix}y_1\\\hat{y}_2\\\hat{y}_3\end{bmatrix}\end{pmatrix}^{2}\)
由于要求咱么输出的loss是一个标量,因此需要将这个\(loss\)进行求和操作。
用MSE的方式求loss这个MSEloss也是继承nn下的module,计算图
torch.nn.MSELoss(size_average = True , reduce=Ture)
- 是否需要求均值
- 是否需要计算聚合的标量损失值,所谓聚合就是求和罢了。
注意这个里面的东西已经被弃用了现在合成了一个reduction
- reduction='mean': 等价于 reduce=True 且 size_average=True。计算批次的平均损失。
- reduction='sum': 等价于 reduce=True 且 size_average=False。计算批次的总和损失。
- reduction='none': 等价于 reduce=False。不进行聚合,返回每个样本的损失。
优化器
这个parameter会检查这里面的所有成员,如果有相应的权重,那么直接就加到咱们的训练结果上面。
- criterion = torch.nn.MSELoss(size_average=False)
- optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
forward, backward, update,
将这个训练数据送进去
一定要注意梯度的归零操作。
然后进行反向传播
- \(\hat{y}\)
- \(loss\)
- \(backward\)
- \(upade\)
最后打印这个运行的日志。
- for epoch in range(100):
- y_pred = model(x_data)
- loss = criterion(y_pred, y_data)
- print(epoch, loss)
- optimizer.zero_grad()
- loss.backward()
- optimizer.step()
- import numpy as np
- import matplotlib.pyplot as plt
- import torch
- # 1 训练数据准备
- x_data = torch.tensor([[1.0] , [2.0] , [3.0]])
- y_data = torch.tensor([[2.0] , [4.0] , [6.0]])
- # 2 设计模型 线性模型 y=x*w+b loss 求和平方函数
- class LinearModel(torch.nn.Module):
- def __init__(self):
- super(LinearModel , self).__init__()
- self.linear = torch.nn.Linear(1,1) # 定义线性模型 y = w*x + b
- def forward(self , x):
- y_pred = self.linear(x) # 直节调用self.linear()这个方法
- return y_pred
-
- Model = LinearModel() # 模型进行实例化
- # 3 定义损失函数并确定优化器
- criterion = torch.nn.MSELoss(size_average=False) # sum
- optimizer = torch.optim.SGD(Model.parameters(),lr =0.05)
- # 4 开始进行学习
- loss_list = []
- epoch_list = []
- w_list = []
- b_list = []
- for epoch in range(0 , 51 , 1):
- epoch_list.append(epoch)
- y_pred = Model(x_data)
- loss = criterion(y_pred , y_data)
- loss_list.append(loss.item()) # 转换成标量
- optimizer.zero_grad()
- loss.backward()
- optimizer.step()
- w_list.append(Model.linear.weight.item())
- b_list.append(Model.linear.bias.item())
- # 日志打印
- for e,l,w ,b in zip(epoch_list , loss_list , w_list , b_list):
- print(f'第{e}轮的时候,损失为{l:.6f},权重为{w:.6f} , 偏置为{b:.6f} \n')
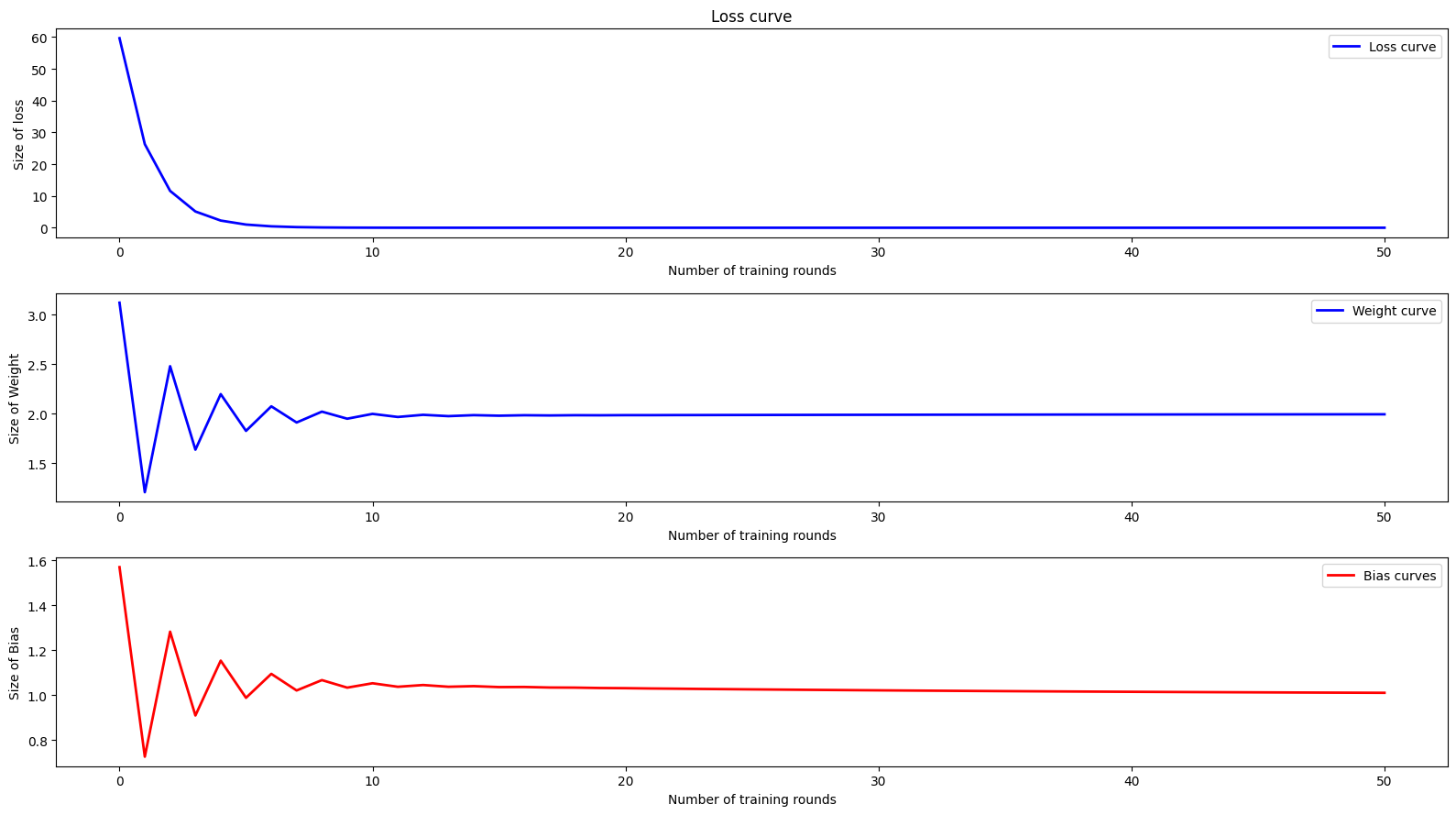
- fig , axes = plt.subplots(3,1 , figsize =(5, 6))
- axes[0].plot(epoch_list , loss_list , 'b-' , linewidth = 2 , label = 'Loss curve')
- axes[0].set_xlabel('Number of training rounds')
- axes[0].set_ylabel('Size of loss')
- axes[0].set_title('Loss curve')
- axes[0].legend()
- axes[1].plot(epoch_list,w_list,'b-',linewidth=2 , label = 'Weight curve')
- axes[1].set_xlabel('Number of training rounds')
- axes[1].set_ylabel('Size of Weight')
- axes[1].legend()
- axes[2].plot(epoch_list,b_list,'r-',linewidth=2 , label = 'Bias curves')
- axes[2].set_xlabel('Number of training rounds')
- axes[2].set_ylabel('Size of Bias')
- axes[2].legend()
- plt.tight_layout()
- plt.show()
注意pytorch有很多优化器:
- torch.optim.Adagrad
- torch.optim.Adam
- torch.optim.Adamax
- torch.optim.ASGD
- torch.optim.LBFGS
- torch.optim.RMSprop
- torch.optim.Rprop
- torch.optim.SGD
pytorch官方文档
总结
这一次咱们主要使用了pytorch进行线性模型的学习操作,让我们再一次回顾一下各类操作,以及深度学习的流程。
1 深度学习的流程
实际上深度学习的流程就那么四个
- 确定并导入训练数据。
- 确定并设计训练模型。
- 给定损失函数以及优化器。
- 进行训练,打印日志,绘制图表。
2. 代码处理
根据上面四部,我们再一次比较清晰粗略的以线性模型为例子,进行说明。
1 确定并导入训练模型。
2 确定并设计训练模型。
3 给定损失函数以及优化器。
4 进行训练
打印日志
绘制图表
可见其实使用pytorch进行深度学习是非常的清晰的。我们最终要的就是对其中的第二步和第三步进行琢磨和处理。
3 函数总结
最后的最后让我把这一次使用到的函数进行一个总结
torch.tensor()
创建一个PyTorch张量(Tensor),这是PyTorch中最基本的数据结构。
- 类似于NumPy的ndarray,但可以在GPU上运行
- 支持自动求导(Autograd)
- 是深度学习计算的基础单元
torch.nn.Linear()
创建一个全连接层(线性层),执行线性变换:y = xA^T + b
参数:
- in_features:输入特征数
- out_features:输出特征数
- bias:是否使用偏置项(默认为True)
内部参数:
- .weight:权重矩阵,形状为 (out_features, in_features)
- .bias:偏置向量,形状为 (out_features,)
torch.nn.MSELoss()
算均方误差损失\((Mean Squared Error Loss)\),用于回归问题。
公式:\(\mathrm{MSE}=\frac{1}{N}\sum_{i=1}^N(y_i-\hat{y}_i)^2\)
参数:
- reduction:指定缩减方式
- 'mean':返回损失的均值(默认)
- 'sum':返回损失的总和
- 'none':不缩减,返回每个元素的损失
torch.optim.SGD()
实现随机梯度下降优化算法。
参数:
- params:需要优化的参数(通常来自model.parameters())
- lr:学习率(learning rate)
- momentum:动量系数(可选,默认为0)
- weight_decay:权重衰减(L2正则化,可选)
.zero_grad()
将模型参数的梯度清零。
.backward()
自动计算梯度(反向传播)
Model.linear.weight.item()
从权重张量中提取标量值。
分解:
- Model.linear:访问模型中的linear层
- .weight:获取该层的权重参数(是一个张量)
- .item():将单元素张量转换为Python标量
Model.linear.bias.item()
从偏置张量中提取标量值。
分解:
- Model.linear:访问模型中的linear层
- .bias:获取该层的偏置参数(是一个张量)
- .item():将单元素张量转换为Python标量
来源:程序园用户自行投稿发布,如果侵权,请联系站长删除
免责声明:如果侵犯了您的权益,请联系站长,我们会及时删除侵权内容,谢谢合作! |