引言
本文原名为《圆方树学习笔记 & 最短路题解》,原始版本可见文末。
本文旨在系统梳理 圆方树(Block forest) 及其思想在图论问题中的应用,尤其是在信息学奥林匹克竞赛(OI)中的实际价值。
我们将从一种特殊的图结构——仙人掌图(Cactus Graph)出发,逐步扩展至一般无向图,分析如何通过构造圆方树,来将复杂图上问题转化为树上问题,并借助经典算法(如树形 DP、树链剖分、DDP、虚树等)解决。
本文对涉及的问题进行了系统归类,并配有例题与代码,构建出一套完整的知识体系,帮助读者深入理解核心思想并掌握其在实际题目中的变形与拓展。当然,并非所有问题都需要显式构造圆方树,部分情况下我们仅借助其结构思想进行分析和维护。
在此基础上,本文还创新性地提出了「圆树」这一辅助结构的概念,以优化特定类型问题的建模与求解过程。
希望本笔记能为正在学习相关内容的读者提供一套完整、实用的参考资料。
全文约二十万字符,除代码外有五万字,因此建议阅读的同时做题来巩固知识。
问题引入
在处理无向图上的复杂问题时,我们常借助图的结构性质进行化简,在简化后的图上使用算法解决问题。比如,使用 Tarjan 算法对图进行缩点:
- 强连通分量缩点后可构成一个有向无环图(DAG);
- 边双连通分量缩点后可转化为一棵树;
- 那么,点双连通分量缩点之后,会变成什么结构?
答案是:圆方树(Block forest)。
圆方树正是对图进行点双连通分量缩点后的结构表示。它将原图中复杂的连通关系映射为树上的结构,从而使许多原本难以处理的问题得以简化为树上问题,显著降低分析与求解的难度。
圆方树的定义
在一张无向图中,对每个点双连通分量建立一个对应的超级节点,并将该分量中所有原图中的点与该超级节点相连,随后删除原图中的所有边。在构建完成后:
- 将这些新增的超级节点称为 「方点」;
- 将原图中的普通节点称为 「圆点」;
这样得到的一棵圆点与方点交错连接的树结构,即为该图的圆方树。
在圆方树上,一个方点的父亲一定是圆点,我们称这个圆点为它的 「父亲圆点」,类似定义 「孩子圆点」,对于一个圆点类似定义 「父亲方点」,「孩子方点」。
以下展示的是一张无向图及其对应的圆方树结构。例如,原图中点双 \(\{2,3,4,5\}\) 对应超级节点 \(15\),在圆方树中,\(15\) 和 \(2,3,4,5\) 都连有边。
本文中,若无特殊说明,认为「两点被一条边连接」这种图结构 是一个点双,如上图中 \(\{8,9\}\)。并为这种点双同样创建一个方点。即在圆方树上不会出现两个圆点直接相连的情况,即不出现圆圆边。
圆方树的简单性质
我们首先需要对圆方树的基本特点有一定了解。
- 圆方树节点数小于 \(2n\),其中 \(n\) 为原图点数。
一个点双引入一个方点,一张图的点双最多只有 \(n-1\) 个,这个上界在图退化为树的情况下达到。所以代码中不要忘记给相关数组开两倍大小。
- 圆方树上一种类型的点只会和另一种类型的点连边。
方点只会和圆点连边,圆点只会和方点连边。由定义不难得到这一点。
- 圆方树上任意一条树链都是「圆方交错」的。
结合上一条性质,不难发现这个性质。
圆方树构建方式
一种简洁而典型的圆方树建树方法是:在运行 Tarjan 算法求点双连通分量的同时构造圆方树。并且可以直接把圆方树建成一棵外向树,便于后续树上遍历。我们直接让方点从 \(n+1\) 开始编号,圆点保持原图上的编号。- void tarjan(int u, int fr) {
- dfn[u] = low[u] = ++timer;
- stack[++top] = u;
- for (int i = G.head[u]; i; i = G.edge[i].nxt) {
- if (i == (fr ^ 1)) continue;
- int v = G.edge[i].v;
- if (!dfn[v]) {
- tarjan(v, i);
- low[u] = min(low[u], low[v]);
- if (low[v] >= dfn[u]) {
- ++dcc_cnt;
- while (true) {
- int x = stack[top--];
- T.add(dcc_cnt + n, x); // 连边:方点 -> 圆点
- if (x == v) break;
- }
- T.add(u, dcc_cnt + n); // 连边:圆点 -> 方点
- }
- } else {
- low[u] = min(low[u], dfn[v]);
- }
- }
- }
圆方树维护点对间所有简单路径信息
关于原图中两点 \(u,v\) 之间所有的简单路径,我们可以将其映射到圆方树上 \(u,v\) 之间的树链,并且借助圆方树的树形结构,来维护这些所有简单路径的信息和。
点对间所有简单路径信息
对于圆方树的映射方式,等到我们分析完信息维护的方式,就呼之欲出了。
我们先来看几种典型的信息:\(u,v\) 间最长简单路径长度、\(u,v\) 间简单路径条数、\(u,v\) 间所有简单路径长度之和、所有能被某一条 \(u,v\) 间简单路径经过的点权和。
我们可以大致分为如下两类。
类型一:满足分配率的边权、点权相关信息
让我们尝试用形式化的语言来形容,进行适当抽象。
设 \(p_i(u,v)\) 表示某一条 \(u\rightarrow v\) 的简单路径。对于这一条简单路径的信息,如果可以看做其中每一条边 \(e\in p_i(u,v)\) 的信息 \(\operatorname{info}(e)\) 按照一种特定的合并方式 \(\odot\) 合并后的结果,我们就称这种信息为 「边权相关信息」,即路径 \(p_i(u,v)\) 的信息为 \(\operatorname{info}(p_i(u,v)) = \bigodot\limits_{e\in p_i(u,v)}\operatorname{info}(e)\)。类似定义点权相关信息,处理这种信息,可以把所有点的点权按照一种方式变成边权,除了某一点需要特殊考虑,剩下维护的就是边权相关信息。因此为了简化讨论,仅考虑边权相关信息。例如:「路径长」是边权相关信息,对于一条边 \(e\),\(\operatorname{info}(e)\) 就是 \(e\) 的长度 \(\operatorname{len}(e)\),\(\odot\) 即为 \(+\),\(\operatorname{info}(p_i(u,v)) = \bigodot\limits_{e\in p_i(u,v)}\operatorname{info}(e) = \sum\limits_{e\in p_i(u,v)}\operatorname{len}(e)\)。
所求的是对于 \(u,v\) 间所有简单路径的信息,按照 \(\oplus\) 合并后的结果,即 \(\operatorname{info}(u,v)=\bigoplus_i\operatorname{info}(p_i(u,v))\)。\(\oplus\) 显然需要满足交换律,否则答案就不唯一了。例如,对于「最长简单路径长度」,就是「路径长」通过 \(\max\) 合并后的信息,\(\odot=+\),\(\oplus=\max\),\(\operatorname{info}(u,v)=\max_i\operatorname{info}(p_i(u,v))=\max_i\sum\limits_{e\in p_i(u,v)}\operatorname{len}(e)\)。
明确需要求解什么后,考虑如何维护。
考虑什么情况下可能可以合并 \(\operatorname{info}(u,v)\) 与 \(\operatorname{info}(v,w)\) 得到 \(\operatorname{info}(u,w)\)。发现当且仅当 \(v\) 是割点的时候,合并信息,才可能得到不重不漏的的结果。因为 \(v\) 作为割点,\(u\rightarrow w\) 的每一条简单路径总是可以拆分成 \(u\rightarrow v\) 和 \(v\rightarrow w\) 两条仅在 \(v\) 处相交的简单路径。这是类似于卷积的,即对于所有 \(i,j\),\(p_i(u,v)\sim p_j(v,w)\) 拼出了一条 \(p_k(u,w)\),并且这种 \(i,j\mapsto k\) 的映射是唯一的。那么 \(\operatorname{info}(u,w)=\bigoplus_k\operatorname{info}(p_k(u,w))=\bigoplus_{i,j}\operatorname{info}(p_i(u,v)\sim p_j(v,w))\)。
在树上,因为 \(u\rightarrow v\) 和 \(v\rightarrow w\) 的简单路径是唯一的,我们有 \(\operatorname{info}(u,w)=\operatorname{info}(u,v)\oplus\operatorname{info}(v,w)\),这是简单的。但是此时 \(u\rightarrow v\) 和 \(v\rightarrow w\) 的简单路径不是唯一的,就不能直接通过 \(\oplus\) 合并了。
有时候我们能够找到一种运算 \(\otimes\),使得我们可以打开这个 \(\bigoplus\),直接合并两个子问题的信息。它需要满足 \(\bigoplus_{i,j}\operatorname{info}(p_i(u,v)\sim p_j(v,w))=\Big(\bigoplus_{i}\operatorname{info}(p_i(u,v))\Big)\otimes\Big(\bigoplus_{j}\operatorname{info}(p_j(v,w))\Big)\),也就是通过 \(\otimes\) 类似树上直接合并两个子问题的信息。把 \(\operatorname{info}\) 用 \(\odot\) 表示,也就是 \(\bigoplus_{i,j}\bigodot_{e\in p_i(u,v)\sim p_j(v,w)}\operatorname{info}(e)=\Big(\bigoplus_{i}\bigodot_{e\in p_i(u,v)}\operatorname{info}(e)\Big)\otimes\Big(\bigoplus_{j}\bigodot_{e\in p_j(v,w)}\operatorname{info}(e)\Big)\)。为了方便观察,不妨用 \(S_i\) 表示 \(p_i(u,v)\),\(T_i\) 表示 \(p_i(v,w)\),等式变为:\(\bigoplus_{i,j}\bigodot_{e\in S_i\cup T_j}\operatorname{info}(e)=\Big(\bigoplus_{i}\bigodot_{e\in S_i}\operatorname{info}(e)\Big)\otimes\Big(\bigoplus_{j}\bigodot_{e\in T_j}\operatorname{info}(e)\Big)\)。用 \(f_i\) 表示 \(\bigodot_{e\in S_i}\operatorname{info}(e)\),\(g_j\) 表示 \(\bigoplus_{j}\bigodot_{e\in T_j}\operatorname{info}(e)\),上等式变成:\(\bigoplus_{i,j}\Big(f_i\odot g_j\Big)=\Big(\bigoplus_{i}f_i\Big)\otimes\Big(\bigoplus_{j}g_j\Big)\)。这个形式很像分配律,进一步,我们可以断言,当且仅当 \(\odot\) 对 \(\oplus\) 满足 分配律 时,\(\otimes\) 存在,且 \(\otimes\) 就是 \(\odot\) 本身,此时,\(\odot\) 和 \(\oplus\) 构成一个 半环。
例如,当 \(\odot=+\),\(\oplus=\max\) 时,\(+\) 对 \(\max\) 满足分配律,此时 \(\otimes\) 存在,且 \(\otimes=\odot=+\)。实际图论意义也很好理解,\(u\rightarrow w\) 所有简单路径中的最长的长度,即为 \(u\rightarrow v\) 和 \(v\rightarrow w\) 分别找到两条最长的拼起来。当 \(\odot=\times\),\(\oplus=+\) 时,\(\times\) 对 \(+\) 满足分配律,此时 \(\otimes\) 存在,且 \(\otimes=\odot=\times\)。当 \(\odot=\oplus=+\) 时,\(+\) 对 \(+\) 不满足分配律,我们找不到 \(\otimes\) 这个运算吗?若仅记录「边权相关信息」,我们确实找不到这样一个运算。但是在后文,我们通过扩展信息的方式,找到了维护这种信息的方式。
有了合并信息的方式,我们要考虑 「原子信息」,即小到不能再小的信息,此时就是 \(u,w\) 处在同一个点双的时候,我们不能找到一条连接 \(u,w\) 的简单路径通过某一个割点 \(v\),于是不能通过合并信息的方式得到 \(u\rightarrow w\) 的信息。不妨对于处于同一点双中的 \(u,w\),用 \(\operatorname{info}(u,w)\) 表示 \(u,w\) 之间的原子信息。原子信息通常是能够方便处理出来的。
我们已经学会了如何维护 \(\odot\) 对 \(\oplus\) 满足分配律的「边权相关信息」、「点权相关信息」。
类型二:非权值相关信息或 \(\odot=\oplus\) 的权值相关信息
此时只存在 \(\otimes\) 这个合并运算。预处理出原子信息同样通常是简单的。例如对于「简单路径条数」,\(\otimes\) 就是 \(\times\)。
上文中遗留一个问题,当 \(\odot=\oplus=+\) 时,由于 \(+\) 对其自身不具有分配律时,不能直接通过「边权相关信息」的方式维护。考虑扩展信息,设 \(\operatorname{info}(u,v)=(s,c)\),其中 \(s\) 表示所求的「所有简单路径长度之和」,\(c\) 表示 \(u\rightarrow v\) 简单路径条数。我们惊喜地发现,有 \((s_1,c_1)\otimes(s_2,c_2)=(s_1c_2+s_2c_1,c_1\cdot c_2)\),这是可以维护的!式子的意义是,对于每一条 \(p_i(u,v)\),由于有 \(c_2\) 条 \(p_j(v,w)\),所以 \(s_1\) 会贡献 \(c_2\) 次。
推广到到一般情况,当 \(\odot=\oplus\) 且对自身不具有分配律时,由于 \(\oplus\) 具有交换律,那么 \(\odot\) 也具有交换律,我们总是可以多记录一个 \(c\),有 \((s_1,c_1)\otimes(s_2,c_2)=\Big((\odot_{c_2}(s_1))\odot(\odot_{c_1}(s_2)),c_1\cdot c_2\Big)\),其中 \(\odot_{k}(x)=\underbrace{x\odot x\odot\cdots\odot x}_{k\text{ 个 }x}\)。
还有另一种可能需要维护的信息,即求能被任意一条 \(u\rightarrow v\) 简单路径经过的所有点 / 边的权值和,这个问题其实非常好处理,只需令 \(\otimes=\oplus\) 即可,这样就能统计到所有点 / 边的权值和,这和树上十分类似。
总结
以上几种信息,在处理完原子信息后,最后都是需要在一个个割点处,将信息通过 \(\otimes\) 合并起来,这正是圆方树可以解决的。
支持查询信息
让我们回到圆方树上,看看它对我们维护信息有什么帮助。
对于 \(u\rightarrow v\) 路径上的信息,可以将路径拆分成不断从一个点双走到另一个点双的过程,即 \(w_1 \stackrel{d_1}{\longrightarrow} w_2\stackrel{d_2}{\longrightarrow} w_3\stackrel{\cdots}{\longrightarrow} w_{m-1}\stackrel{d_{m-1}}{\longrightarrow}w_m\),其中 \(w_1=u, w_m=v\),对于 \(i=1,\ldots,m-1\),\(w_{i},w_{i+1}\) 分别是编号为 \(d_i\) 的点双中两个点。根据上述讨论,我们要求的就是 \(\bigotimes\limits_{i=1}^{m-1}\operatorname{info}(w_i,w_{i+1})\),而每个 \(\operatorname{info}(w_i,w_{i+1})\) 均为原子信息。
\(w_i\stackrel{d_i}{\longrightarrow}w_{i+1}\) 是走进一个点双,再从中走出来,圆方树上,我们为每个点双建立了一个方点,这不就相当于从 \(w_i\) 走到 \(d_i\) 对应的方点,再走到 \(w_{i+1}\) 吗?进一步地,这不就构成了圆方树上一条以 \(u,v\) 为端点的树链了吗?我们于是自然得出了圆方树和原图之间的对应关系:
- 圆方树上一条「圆方圆」的路径,对应原图点双中两点之间所有简单路径。
比如上图中 \(\{3,15,5\}\) 这条圆方圆路径,对应原图中 \(\{2,3,4,5\}\) 这个点双中以 \(3,5\) 为端点的所有简单路径,即 \(\{3,2,5\},\{3,4,5\}\) 两条简单路径。
这就是进入一个点双,再从这个点双中走出来。
- 圆方树上任意一条树链 \((u,v)\) 对应原无向图中 \(u,v\) 之间所有简单路径。
比如上图中 \((3,8)\) 这条树链,对应了原图中 \(\{3,2,5,9,8\},\{3,2,5,6,9,8\},\{3,4,5,9,8\},\{3,4,5,6,9,8\}\) 这些简单路径。
这种把每一条「圆方圆」的路径合并起来的过程,对应不断从一个点双走到另一个点双的过程。
圆方树很好地刻画了通过 \(\otimes\) 合并信息的过程!让我们继续分析。
对于一次查询 \((u,v)\),设 \(p=\operatorname{lca}(u,v)\),将树链拆分成 \(u\rightarrow p\rightarrow v\)。考虑 \(u\rightarrow p\) 一侧,另一侧类似。
考虑如下圆方树一部分:
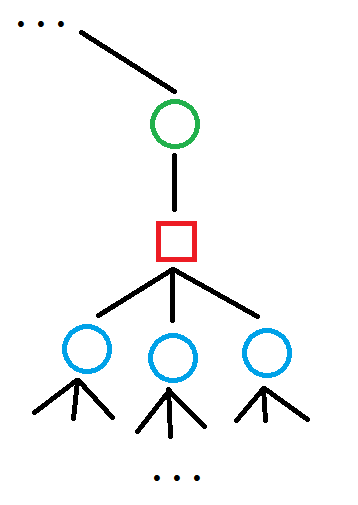
当我们经过某一个圆点(蓝点)\(u\),跳向它爷爷(绿点)\(v\) 时,需要求的是 \(u\) 和 \(v\) 的原子信息 \(\operatorname{info}(u,v)\)。不考虑修改的情况下,每一次从 \(u\) 跳到 \(v\),原子信息都是相同的,因为它的爷爷 \(v\) 是唯一的。我们于是这可以预处理出这些原子信息,而这类原子信息的个数和非根圆点个数相同,是 \(\mathcal{O}(n)\) 的。我们将 \(u\) 和 \(v\) 的信息,放在 \(u\) 到它父亲方点(红点)的边权上,每个方点和它父亲圆点之间的边权设为单位元。那么我们考虑一对具有祖孙关系的节点,他们之间的信息,便是圆方树上他们之间边权按序合并的结果。
对于 \(u\rightarrow p\) 和 \(p\rightarrow v\) 两段,根据我们赋的边权,和我们之前学过的树上信息维护方式,这两段路径的信息已经可以求出。对于不满足交换律的信息,可能需要维护向上跳的信息和向下跳的信息。接下来,好像直接把这两个信息合并起来就是对的,其实不然。对于 \(p\) 是圆点的情况,这么做是正确的;但是对于 \(p\) 是方点的情况,设 \(u'\) 为 \(p\) 的孩子且是 \(u\) 的祖先,\(v'\) 同理,那么考虑直接合并信息的实际意义,是从 \(u\) 走到 \(u'\),进入了 \(p\) 对应的点双,走到了 \(\operatorname{fa}(p)\),再走进 \(p\) 对应的点双,走到 \(v'\),最终到 \(v\)。这显然是错误的,我们要求 \(u'\rightarrow v'\) 的原子信息 \(\operatorname{info}(u',v')\),而非 \(\operatorname{info}(u',\operatorname{fa}(p))\otimes\operatorname{info}(\operatorname{fa}(p),v')\)。解决方式很简单,只需要特殊查询一次 \(u'\rightarrow v'\) 的原子信息,和之前两个信息合并。
在实现上,我们需要支持询问点双内两点之间的原子信息,那么这是否意味着需要为每个点记录其所在所有点双内的信息?如果真的需要,我们可以为每一个元素开 \(m+1\) 个 vector,其中 \(m\) 个 vector info 用来记录信息,\(1\) 个 vector id 用来存所有 \(u\) 点双的编号,意为 \(u\) 在编号为 id 的点双内对应的信息为 info,对于查询 \(u\) 在编号为 \(x\) 的点双中的信息,先在 id 中二分出 \(x\) 的下标,再拿这个下标去访问 info。但是这是不必要的,这是因为我们的查询并不真的「任意」,而是只会查询一个圆点,在其父亲方点对应点双中的信息。而每个孩子圆点的父亲是唯一的,如果他被查询到,所用到的信息也是唯一的,那就不需要使用 vector 了。vector 的写法请参考下文仙人掌部分例五代码。
至此,我们借助圆方树的特殊结构,结合树上信息维护方式,通过 \(\otimes\) 的合并方式,可以查询给定点对间所有简单路径的信息。
支持修改信息
如果有了修改呢?树上我们使用树剖来支持修改查询树链信息,那么接下来要做的就是把圆方树剖开,尝试在上面维护信息。
先来考虑一种特殊的信息,求 \(u\rightarrow v\) 能到达的所有点的点权的信息和。这时候同一个点双内 \(u\rightarrow v\) 的信息为点双中除去 \(v\) 的点权信息和。发现圆方树上的边权很有规律,对于一个方点,它连向所有孩子圆点的边权总是相同的,都是该点双中除去父亲圆点的点权信息和。我们把边权上放,给方点一个点权(注意和原点权加以区分),为原先我们给圆方树赋的边权,再把圆点的点权设置为单位元。我们的查询似乎就变成了圆方树上路径的点权信息之和。
考虑在 LCA 处的特殊情况。若 LCA 为方点,同样需要得到 \(u'\rightarrow v'\) 的信息。如果严格遵循上文对原子信息的定义,我们需要先扣掉 \(v'\) 的点权,但是这样到最后会漏掉 \(v'\) 的点权(点权转换后的特殊情况),所以我们完全不必扣掉 \(v'\) 的点权,而是查出 LCA 的点权后,再加上 LCA 父亲圆点的点权。对于 LCA 为圆点的情况,我们统计漏了这个 LCA 圆点的信息,这把它的点权贡献到答案里就好了。如此就完成了查询。
修改某个点的权值的时候,除了需要维护仙人掌上每个点的点权,还要修改其在圆方树上父亲方点的点权。要想快速得到新的点权,要对每一个方点维护一个支持插入删除的数据结构,每次先删除原先的贡献,再加入修改后点权的贡献即可。
我们现在只需要在一棵树上,支持修改点权,询问 \(\operatorname{lca}\),询问路径点权和。这个可以树剖做到 \(\log^2\),或者可以做到单 \(\log\)。另外,理论上来说,我们还可以继续上放点权,也就是在圆树操作。但是这会造成很多边界情况,不优雅,故不展开讨论。
考虑更为一般的情况。我们发现边权上放的本质是为了修改的时候,能够将父亲方点的所有孩子圆点往上跳的边权都修改。但是真的一定需要更新每个孩子圆点吗?并不是,我们只需要修改重孩子圆点。每次跳重链时,只需要考虑链顶这个轻儿子的特殊情况。于是完成了修改和维护信息。
「圆树」:不设置方点的可行性
上文中,方点的作用仅是用来判断 \(u'\) 和 \(v'\) 是否在同一点双内,在一些简单的问题中,我们确实可以不建出方点,只建出「圆树」,并在每个点记录它在圆方树上父亲方点是谁,在查询的时候,只需要要找出 \(u',v'\)(如果存在的话),然后判断他们的父亲圆点是否相同,就能知道 LCA 是方点还是圆点。
优点
- 节点总数为 \(n\):
不引入新的方点,整棵树的节点数量保持为原图大小的 \(n\),在最坏情况下仅为传统圆方树节点数的一半。这样可以节省时间空间,而且不会因为手残数组开小,或者预处理只处理到 \(n\) 而红温。
- 实现简单:
若采用倍增算法来维护树上信息和求 LCA,当一个节点是另一个节点的祖先时,不会出现 LCA 是方点的特殊情况。剩下来的情况,我们倍增本来就是先求出了 \(u',v'\),然后再跳最后一步到 LCA 的,那我们在跳之前判断一下就好了,不必等到跳了才发现是同一个方点。
缺点
- 过度依赖倍增:
若题目采用树上前缀和、差分等方式来维护信息,通常使用基于 DFS 序的 \(\mathcal{O}(1)\) LCA 算法,而寻找 \(u', v'\) 却是 \(\mathcal{O}(\log n)\) 的,导致效率不匹配。除非你愿意使用如长链剖分实现 \(\mathcal{O}(1)\) 的 kth-father 查询:先求出 LCA,再通过深度差计算 \(u'\) 或 \(v'\),这会显著增加代码复杂度。
发明了基于 DFS 序 \(\mathcal{O}(1)\) 求 \(u',v'\) 的算法,可见:博客。
- 在特定情况下有过多边界问题:
例如维护需要支持修改的信息,使用圆树将需要很多分类讨论,万一没有讨论所有情况,就会出错,而且代码将变得难以理解。
- 过于小众:
求调的时候别人说看不懂。
总而言之,这是仅是一种小优化,在掌握了圆方树的基本构造与思想后,读者可根据题目类型与实现习惯,自行选择是否采用此优化版本。
圆树和圆方树两种写法,在例题五和例题十三均分别给出,供参考对比。
圆方树在「仙人掌」上的应用
我们先从 仙人掌 这种特殊的无向图开始研究圆方树,这是因为仙人掌具有十分良好的性质。
初识仙人掌
仙人掌的定义
仙人掌指任意一条边最多出现在一个简单环中的无向连通图。
仙人掌的性质
- 仙人掌边数上界为 \(\mathcal{O}(n)\)。
准确来说,为 \(2n-2\) 或 \(\lfloor\frac{3}{2}(n-1)\rfloor\)。
当允许重边时,把一棵树的所有 \(n-1\) 条树边,复制一遍,得到一棵 \(2n-2\) 条边的仙人掌。注意不可能出现三条重边连接两个点,否则就不满足仙人掌的定义了。
当不允许重边时,可以发现如下「类菊花」的结构使得边数达到最多,为 \(\lfloor\frac{3}{2}(n-1)\rfloor\)。
- 仙人掌具有类似树的结构。
我们发现,由于仙人掌的环不交(准确的说为边不交),这使得其保留了树的一些形态。
把每一个环看做一个巨大的节点,仙人掌就成了一棵树了,只不过有些节点间不依靠边相连,而是在公共点处相切。
类似树上「子树」,我们可以定义「子仙人掌」。
「子仙人掌」指定一个根,定义 \(u\) 的「子仙人掌」为,断开根和 \(u\) 的所有简单路径的边后,\(u\) 所在的连通块。
不难发现,\(u\) 的「子仙人掌」对应圆方树上 \(u\) 的子树。画个图就十分清晰了:
不难做进一步推广,类似在一般无向图上定义「子无向图」,容易发现,这同样对应圆方树的子树。
类似树上「树链」,在 只存在奇环 的仙人掌上,由于最长 / 短路唯一,我们可以定义「长链」、「短链」的概念。
「长链」、「短链」\(u,v\) 之间经过边数最多的的简单路径称为 \(u,v\) 间的「长链」;\(u,v\) 之间经过边数最少的简单路径称为 \(u,v\) 间的「短链」。
显然,在仙人掌中每经过一个环时,若都选择在环上走最长(或最短)路径,则整条走出的路径即为 \(u, v\) 间的长链(或短链)。
需要注意仙人掌上的点双并 不一定是环,通过一条不在环上的边连接的两个点,构成了两个点的点双,而这个点双不是一个环。有时候我们需要特判这种情况。
仙人掌上构造圆方树
我们可能需要在构造圆方树的时候,维护当前环的形态,即得到当前环对应的子图。
方法一:树上前缀和
一种做法是,对每个节点维护在 tarjan 的 dfs 树上的树上前缀和(即到根的信息),对于在 dfs 树上 \(u\) 是 \(v\) 的祖先,用 \(v\) 的前缀和减去 \(u\) 的前缀和,就能得到 \(u\) 到 \(v\) 之间的信息。那我们选用父亲圆点 \(u\) 作为环首,这样环上每一个点都处于 dfs 树中 \(u\) 的子树中,于是可以得到每个点到环首 \(u\) 的信息。至于总环长,发现我们上述过程考虑的是一条以 \(u\) 为环首的一条链,对于环尾 \(v\),他有且仅有一条返祖边,且这条返祖边恰连向 \(u\),从而构成一个环。一个点不可能有两条或以上返祖边,否则不满足仙人掌的定义。而这个返祖边我们可以轻松维护。如下图,蓝色的边为 dfs 树树边,红色的边为返祖边,细黑边为圆方树上的树边。当前的环即为若干条蓝边和一条红边构成的环。绿色箭头表示环首走向环尾的方向,蓝紫色箭头指向形成闭环的那条环尾指向环首的边。
方法二:弹边栈
这种做法对于不可差分信息不太好处理,并且依赖于环这种形态,不好向一般点双拓展。考虑类似点的栈,维护一个边的栈,存返祖边和树边,在 tarjan 的过程中,每次找到一个点双(\(\operatorname{low}(v) \geq \operatorname{dfn}(u)\)),就不断弹栈,直到弹出连接 \(u,v\) 的树边(注意必须是树边)。这个过程中弹出的边,便构成了这个点双的子图。对于复杂一些的点双,我们需要建出这个子图,然后在这个子图上跑一些算法,但是于仙人掌而言,我们把一个环建出来再处理,未免小题大做了。我们发现按照弹栈的顺序,弹出的边依次为环中的返祖边,深度最深的树边,深度次深的树边,直到 \(u,v\) 之间的树边。更加优雅的做法是,我们按照弹栈的顺序,假设当前弹出的边为 \(u'\rightarrow v'\),边权为 \(w\),并且不是连接 \(u,v\) 的树边,设 \(u\) 在环上的信息前缀和为 \(p_u\),那么就让 \(p_{u'}\gets p_{v'}+w\)。这种方法下,环首为 \(u\),环尾是 \(v\),\(u,v\) 之间的树边成了环尾连向环首的边。如下图。事实上,使用了这种方式,我们不需要原先的点栈,每次弹出的边的起点,相当于原先点栈每次弹出的点。
类型一:单次询问整体信息
计数类问题
在处理计数类问题时,往往需要借助圆方树进行类似树形 DP,或其他类似树上的统计方法。
在普通树上,这类问题我们已非常熟悉;放到基环树上,常见的技巧是将环上 DP 与树形 DP 分开处理,其本质原因是,把环上每个结点看做对应树根,这棵树是一个子问题,所以剩下的部分是一个环上问题。
在仙人掌上,由于我们前文提到的仙人掌具有的类似树的性质,所以在 DP 转移的时候,可以分环上 DP 和树形 DP 进行转移,或者按照环上和树上进行统计答案。这在圆方树上体现为,在方点、圆点上分别处理。
实际上,对于这类问题,我们甚至无需显式构建整棵圆方树。只需在分析与转移过程中设想当前所处的是圆点还是方点,并据此决定转移逻辑,即可完成建模与求解。这也是圆方树思想灵活而强大的体现。
例一、静态仙人掌最大独立集(小 C 的独立集,黑暗爆炸、洛谷、Hydro)Problem Statement给你一个有 \(n\) 个点和 \(m\) 条边的仙人掌,求它的最大独立集大小。
\(n\leq 5\times 10^4\),\(m\leq 6\times 10^4\)。
Problem Analysis树上最大独立集是经典的(猜你想找:没有上司的舞会),我们设 \(f_{u,0/1}\) 表示以 \(u\) 为根的子树这个子问题,\(u\) 选 / 不选,最大独立集为多少。转移为 \(f_{u,0}=\sum\limits_{v\in\operatorname{son}(u)}\max\Big\{f_{v,0},f_{v,1}\Big\}\),\(f_{u,1}=\operatorname{val}(u)+\sum\limits_{v\in\operatorname{son}(u)}f_{v,0}\)。
基环树上最大独立集是经典的(猜你想找:MAFIJA,[ZJOI2008] 骑士),我们先把树形 DP 跑了,得到环上每个点 \(u\) 的 \(f_{u,0/1}\),然后再做一遍环上 DP。如果这个环没有首尾之间的独立集限制,这其实就是一条链,按照树的方式转移即可。但是首尾之间有限制,我们就先钦定首必不能选,然后做一遍 DP,把尾的 \(f_{0/1}\) 算到答案的贡献里,然后钦定首必选(亦可钦定其可选可不选,如果需要求独立集方案,为了不冲不漏,此处要钦定必选),再做一遍 DP,把尾的 \(f_0\) 贡献进去,这里就不贡献 \(f_1\) 了,不然会不满足首尾之间的限制条件。
另外一种基环树 DP 形式有人说,我学的基环树 DP 不太一样,是:把环上一条边拎出来,剩下一棵树,然后类似上面的钦定,做两遍树形 DP。这两种方法其实是本质相同的,只不过这种方法把断边后的环当做树上一条链,整体做一遍 DP,相当于把环上 DP 放在树形 DP 里做了。对于仙人掌来说,我们还是喜欢单独对环做 DP。
那么仙人掌上也很好做了。\(f\) 的定义便是关于 \(u\) 的子仙人掌上的信息。圆点上我们赋初值 \(f_{u,0}\gets 0, f_{u,1}\gets 1\)。在方点上,我们做环上 DP,然后把答案统计到方点的父亲圆点 \(u\) 上。先使得 \(u\) 在环尾,然后类似基环树上的环做两遍 DP,得到 \(f_{u,0/1}\)。在两遍环上的 DP 的时候,不要把答案直接赋给 \(f_u\),而是应该使用临时变量存放,做完两遍 DP 后再存到 \(f_u\) 里面,这样是为了避免第一次 DP 对第二次 DP 造成的影响。
于是,我们做到了时空线性 \(\mathcal{O}(n+m)\) 解决了本题。
做完这题可以去尝试一下 [SDOI2010] 城市规划,树套环上求至少间隔两个位置的最大独立集,可以参考我的题解。
Solution[code]#include #include #include using namespace std;const int N = 5e4 + 10;const int M = 6e4 + 10;int n, m;struct node { int v, nxt;} edge[M = dfn) { // 这里应该会新建一个方点 // 但我们并不需要真的把圆方树建出来 vector scc; while (true) { int x = stack[top--]; scc.emplace_back(x); if (x == v) break; } scc.emplace_back(u); // u 在环尾 int m = scc.size(); int f0 = 0, f1 = 0; // 强制首不选 g[0][0] = f[scc[0]][0], g[0][1] = -0x3f3f3f3f; for (int i = 1; i < m; ++i) { g[0] = max(g[i - 1][0], g[i - 1][1]) + f[scc][0]; g[1] = g[i - 1][0] + f[scc][1]; } f0 = max(f0, g[m - 1][0]); f1 = max(f1, g[m - 1][1]); // 首可选可不选 g[0][0] = f[scc[0]][0], g[0][1] = f[scc[0]][1]; for (int i = 1; i < m; ++i) { g[0] = max(g[i - 1][0], g[i - 1][1]) + f[scc][0]; g[1] = g[i - 1][0] + f[scc][1]; } f0 = max(f0, g[m - 1][0]); f[0] = f0, f[1] = f1; } } else { low = min(low, dfn[v]); } }}int main() { scanf("%d%d", &n, &m); for (int i = 1, u, v; i |