现在使用的电子设备大部分都支持触控操作,如手机、平板电脑,这些设备上的应用基本都依赖触摸事件的一些特性,如根据触摸事件移动速度计算视图控件的动画效果。在Android的API中提供了VelocityTracker类用于计算触摸事件MotionEvent的速度,而其内部默认使用的方法就是最小二乘法,本文主要介绍其实现原理,以便应用到自己的非Android应用中。
匀速运动
如果用\(p(x,y)\) \(t\)表示触摸事件点的坐标和时间,已知两个点\(p_0(x_0,y_0)\) \(p_1(x_1,y_1)\)和时间\(t_0\) \(t_1\),那么可以使用最简单的方法计算触摸事件点的移动速度:
\[\overrightarrow{V_1} = \frac{1}{t_1-t_0}\begin{bmatrix}x_1-x_0 \\y_1-y_0\end{bmatrix}\tag{1}\]
使用这种方法的前提条件是接受触摸事件点是匀速运动,加速度等于零:\(\overrightarrow{A}=0\)
恒定加速度
假定触摸事件点的运动速度为\(v\),加速度为\(a\),时间为\(t\),则触摸事件的运动方程为:
\[y=y_0+vt+\frac{1}{2}at^2\tag{2}\]
现在已知一系列触摸事件点\(p\)和每个触摸点对应的时间\(t\),那么如何求得当前触摸事件点的速度\(v\)和加速度\(a\)呢?
最小二乘法
将运动方程写成矩阵形式:
\[\begin{align}y=&\begin{bmatrix}1 & t & t^2\end{bmatrix} \notag\begin{bmatrix}y_0 \\v \\\frac{1}{2}a\end{bmatrix}\\=&\begin{bmatrix}1 & t & t^2\end{bmatrix}\bm{\beta} \notag\end{align}\tag{3}\]
假设测量(采集)的数据集为:
\[\begin{align}\bm{t} &= \begin{bmatrix} t_0, & t_1, & ..., & t_n \end{bmatrix} \tag{4}\\\bm{X} &= \begin{bmatrix} 1 & t_0 & t_0^2 \\1 & t_1 & t_1^2 \\\vdots & \vdots & \vdots \\1 & t_n & t_n^2 \end{bmatrix} \tag{5} \\\bm{Y} &= \begin{bmatrix} y_0, & y_1, & ..., & y_n \end{bmatrix}^T \tag{6}\\\end{align}\]
如果用\(\hat{\bm{\beta}}\)表示运动模型参数的估计值,那么运动模型结果估计值可以表示为:
\[\hat{\bm{Y}} = \bm{X}\hat{\bm{\beta}} \tag{7}\]
用\(\bm{Y}-\hat{\bm{Y}}\)表示测量(采集)值与估计值之间的误差,那么当误差平方最小时,此时的\(\hat{\bm{\beta}}\)就是需要求取的运动模型参数值:
\[\begin{align}min\Vert \bm{Y} - \hat{\bm{Y}} \Vert^2 &= min\Vert \bm{Y} - \bm{X}\hat{\bm{\beta}} \Vert^2 \notag \\&= \sum_{i=0}^{n}{\big(y_i-(\beta_0+\beta_1t_i+\beta_2t_i^2)\big)^2} \notag\end{align}\tag{8}\]
当上式对\(\beta_0\)、\(\beta_1\) 和\(\beta_2\)进行偏导为0时其值最小:
\[\begin{align}\sum_{i=0}^{n}{y_i} &= \sum_{i=0}^{n}{\big(\beta_0+\beta_1t_i+\beta_2t_i^2\big)}= n\beta_0 + \beta_1\sum_{i=0}^{n}{t_i} + \beta_2\sum_{i=0}^{n}{t_i^2} \tag{9} \\\sum_{i=0}^{n}{y_it_i} &= \sum_{i=0}^{n}{\big(\beta_0t_i+\beta_1t_i^2+\beta_2t_i^3\big)}= \beta_0\sum_{i=0}^{n}{t_i} + \beta_1\sum_{i=0}^{n}{t_i^2} + \beta_2\sum_{i=0}^{n}{t_i^3} \tag{10}\\\sum_{i=0}^{n}{y_it_i^2} &= \sum_{i=0}^{n}{\big(\beta_0t_i^2+\beta_1t_i^3+\beta_2t_i^4\big)}= \beta_0\sum_{i=0}^{n}{t_i^2} + \beta_1\sum_{i=0}^{n}{t_i^3} + \beta_2\sum_{i=0}^{n}{t_i^4} \tag{11}\\\end{align}\]
使用消元法进行求解,先将式\((10)\)和\((11)\)中的\(\beta_0\)消去:
\[\begin{align}\frac{1}{n}\sum_{i=0}^{n}{y_i}\sum_{i=0}^{n}{t_i}- \sum_{i=0}^{n}{y_it_i}&= \beta_0\sum_{i=0}^{n}{t_i}+ \frac{1}{n}\beta_1\sum_{i=0}^{n}{t_i}\sum_{i=0}^{n}{t_i} + \frac{1}{n}\beta_2\sum_{i=0}^{n}{t_i^2}\sum_{i=0}^{n}{t_i}- \beta_0\sum_{i=0}^{n}{t_i}- \beta_1\sum_{i=0}^{n}{t_i^2}- \beta_2\sum_{i=0}^{n}{t_i^3} \notag \\&= \frac{1}{n}\beta_1\sum_{i=0}^{n}{t_i}\sum_{i=0}^{n}{t_i} + \frac{1}{n}\beta_2\sum_{i=0}^{n}{t_i^2}\sum_{i=0}^{n}{t_i} - \beta_1\sum_{i=0}^{n}{t_i^2}- \beta_2\sum_{i=0}^{n}{t_i^3} \notag \\&= \beta_1 \big( \frac{1}{n}\sum_{i=0}^{n}{t_i}\sum_{i=0}^{n}{t_i} -\sum_{i=0}^{n}{t_i^2} \big)+ \beta_2 \big( \frac{1}{n}\sum_{i=0}^{n}{t_i^2}\sum_{i=0}^{n}{t_i} - \sum_{i=0}^{n}{t_i^3}\big) \notag \\\end{align}\tag{12}\]
\[\begin{align}\frac{1}{n}\sum_{i=0}^{n}{y_i}\sum_{i=0}^{n}{t_i^2} - \sum_{i=0}^{n}{y_it_i^2}&= \beta_0\sum_{i=0}^{n}{t_i^2} + \frac{1}{n}\beta_1\sum_{i=0}^{n}{t_i}\sum_{i=0}^{n}{t_i^2} + \frac{1}{n}\beta_2\sum_{i=0}^{n}{t_i^2}\sum_{i=0}^{n}{t_i^2}- \beta_0\sum_{i=0}^{n}{t_i^2} - \beta_1\sum_{i=0}^{n}{t_i^3} - \beta_2\sum_{i=0}^{n}{t_i^4} \notag \\&= \frac{1}{n}\beta_1\sum_{i=0}^{n}{t_i}\sum_{i=0}^{n}{t_i^2} + \frac{1}{n}\beta_2\sum_{i=0}^{n}{t_i^2}\sum_{i=0}^{n}{t_i^2} - \beta_1\sum_{i=0}^{n}{t_i^3} - \beta_2\sum_{i=0}^{n}{t_i^4} \notag \\&= \beta_1 \big( \frac{1}{n}\sum_{i=0}^{n}{t_i}\sum_{i=0}^{n}{t_i^2} -\sum_{i=0}^{n}{t_i^3} \big) + \beta_2 \big( \frac{1}{n}\sum_{i=0}^{n}{t_i^2}\sum_{i=0}^{n}{t_i^2} - \sum_{i=0}^{n}{t_i^4}\big) \notag \\\end{align}\tag{13}\]
再将式\((12)\)和\((13)\)中的\(\beta_1\)消去得到\(\beta_2\):
\[\begin{align}\big(\frac{1}{n}\sum_{i=0}^{n}{y_i}\sum_{i=0}^{n}{t_i} - \sum_{i=0}^{n}{y_it_i}\big)\big( \frac{1}{n}\sum_{i=0}^{n}{t_i}\sum_{i=0}^{n}{t_i^2} -\sum_{i=0}^{n}{t_i^3} \big)- \big(\frac{1}{n}\sum_{i=0}^{n}{y_i}\sum_{i=0}^{n}{t_i^2} - \sum_{i=0}^{n}{y_it_i^2}\big)\big( \frac{1}{n}\sum_{i=0}^{n}{t_i}\sum_{i=0}^{n}{t_i} -\sum_{i=0}^{n}{t_i^2} \big) \notag \\= \beta_2 \big( \frac{1}{n}\sum_{i=0}^{n}{t_i^2}\sum_{i=0}^{n}{t_i} - \sum_{i=0}^{n}{t_i^3}\big)\big( \frac{1}{n}\sum_{i=0}^{n}{t_i}\sum_{i=0}^{n}{t_i^2} -\sum_{i=0}^{n}{t_i^3} \big)- \beta_2 \big( \frac{1}{n}\sum_{i=0}^{n}{t_i^2}\sum_{i=0}^{n}{t_i^2} - \sum_{i=0}^{n}{t_i^4}\big)\big( \frac{1}{n}\sum_{i=0}^{n}{t_i}\sum_{i=0}^{n}{t_i} -\sum_{i=0}^{n}{t_i^2} \big) \notag\end{align} \tag{14}\]
\[\beta_2 = \frac{\big(\frac{1}{n}\sum_{i=0}^{n}{y_i}\sum_{i=0}^{n}{t_i} - \sum_{i=0}^{n}{y_it_i}\big)\big( \frac{1}{n}\sum_{i=0}^{n}{t_i}\sum_{i=0}^{n}{t_i^2} -\sum_{i=0}^{n}{t_i^3} \big)- \big(\frac{1}{n}\sum_{i=0}^{n}{y_i}\sum_{i=0}^{n}{t_i^2} - \sum_{i=0}^{n}{y_it_i^2}\big)\big( \frac{1}{n}\sum_{i=0}^{n}{t_i}\sum_{i=0}^{n}{t_i} -\sum_{i=0}^{n}{t_i^2} \big)}{\big( \frac{1}{n}\sum_{i=0}^{n}{t_i^2}\sum_{i=0}^{n}{t_i}- \sum_{i=0}^{n}{t_i^3}\big)^2- \big( \frac{1}{n}\sum_{i=0}^{n}{t_i^2}\sum_{i=0}^{n}{t_i^2} - \sum_{i=0}^{n}{t_i^4}\big)\big( \frac{1}{n}\sum_{i=0}^{n}{t_i}\sum_{i=0}^{n}{t_i} -\sum_{i=0}^{n}{t_i^2} \big)}\tag{15}\]
将上式中的\(\sum_{i=0}^{n}\)用\(S\)代替,这样可以让公式更加直观:
\[\beta_2 = \frac{\big(\frac{1}{n}S_{y}S_{t} - S_{yt}\big)\big( \frac{1}{n}S_{t}S_{t^2} -S_{t^3} \big)- \big(\frac{1}{n}S_{y}S_{t^2} - S_{yt^2}\big)\big( \frac{1}{n}S_{t}S_{t} -S_{t^2} \big)}{\big( \frac{1}{n}S_{t}S_{t^2}- S_{t^3}\big)^2- \big( \frac{1}{n}S_{t^2}S_{t^2} - S_{t^4}\big)\big( \frac{1}{n}S_{t}S_{t} -S_{t^2} \big)} \\\tag{16}\]
将式\((12)\)和\((13)\)中的\(\beta_2\)消去得到\(\beta_1\):
\[\begin{align}\big( \frac{1}{n}\sum_{i=0}^{n}{y_i}\sum_{i=0}^{n}{t_i} - \sum_{i=0}^{n}{y_it_i} \big)\big( \frac{1}{n}\sum_{i=0}^{n}{t_i^2}\sum_{i=0}^{n}{t_i^2} - \sum_{i=0}^{n}{t_i^4}\big)- \big( \frac{1}{n}\sum_{i=0}^{n}{y_i}\sum_{i=0}^{n}{t_i^2} - \sum_{i=0}^{n}{y_it_i^2} \big)\big( \frac{1}{n}\sum_{i=0}^{n}{t_i^2}\sum_{i=0}^{n}{t_i} - \sum_{i=0}^{n}{t_i^3}\big) \notag \\= \beta_1 \big( \frac{1}{n}\sum_{i=0}^{n}{t_i}\sum_{i=0}^{n}{t_i} -\sum_{i=0}^{n}{t_i^2} \big)\big( \frac{1}{n}\sum_{i=0}^{n}{t_i^2}\sum_{i=0}^{n}{t_i^2} - \sum_{i=0}^{n}{t_i^4}\big)- \beta_1 \big( \frac{1}{n}\sum_{i=0}^{n}{t_i}\sum_{i=0}^{n}{t_i^2} -\sum_{i=0}^{n}{t_i^3} \big)\big( \frac{1}{n}\sum_{i=0}^{n}{t_i^2}\sum_{i=0}^{n}{t_i} - \sum_{i=0}^{n}{t_i^3}\big) \notag\end{align} \tag{17}\]
\[\begin{align}\beta_1 = \frac{\big( \frac{1}{n}\sum_{i=0}^{n}{y_i}\sum_{i=0}^{n}{t_i} - \sum_{i=0}^{n}{y_it_i} \big)\big( \frac{1}{n}\sum_{i=0}^{n}{t_i^2}\sum_{i=0}^{n}{t_i^2} - \sum_{i=0}^{n}{t_i^4}\big)- \big( \frac{1}{n}\sum_{i=0}^{n}{y_i}\sum_{i=0}^{n}{t_i^2} - \sum_{i=0}^{n}{y_it_i^2} \big)\big( \frac{1}{n}\sum_{i=0}^{n}{t_i^2}\sum_{i=0}^{n}{t_i} - \sum_{i=0}^{n}{t_i^3}\big)}{\big( \frac{1}{n}\sum_{i=0}^{n}{t_i}\sum_{i=0}^{n}{t_i} -\sum_{i=0}^{n}{t_i^2} \big)\big( \frac{1}{n}\sum_{i=0}^{n}{t_i^2}\sum_{i=0}^{n}{t_i^2} - \sum_{i=0}^{n}{t_i^4}\big)- \big( \frac{1}{n}\sum_{i=0}^{n}{t_i}\sum_{i=0}^{n}{t_i^2} -\sum_{i=0}^{n}{t_i^3} \big)^2} \notag\end{align} \tag{18}\]
\[\begin{align}\beta_1 = \frac{\big( \frac{1}{n}S_{y}S_{t} - S_{yt} \big)\big( \frac{1}{n}S_{t^2}S_{t^2} - S_{t^4}\big)- \big( \frac{1}{n}S_{y}S_{t^2} - S_{yt^2} \big)\big( \frac{1}{n}S_{t^2}S_{t} - S_{t^3}\big)}{\big( \frac{1}{n}S_{t}S_{t} -S_{t^2} \big)\big( \frac{1}{n}S_{t^2}S_{t^2} - S_{t^4}\big)- \big( \frac{1}{n}S_{t}S_{t^2} -S_{t^3} \big)^2} \notag \\= \frac{\big( \frac{1}{n}S_{y}S_{t^2} - S_{yt^2} \big)\big( \frac{1}{n}S_{t}S_{t^2} - S_{t^3}\big) -\big( \frac{1}{n}S_{y}S_{t} - S_{yt} \big)\big( \frac{1}{n}S_{t^2}S_{t^2} - S_{t^4}\big) }{\big( \frac{1}{n}S_{t}S_{t^2} -S_{t^3} \big)^2 - \big( \frac{1}{n}S_{t^2}S_{t^2} - S_{t^4}\big)\big( \frac{1}{n}S_{t}S_{t} -S_{t^2} \big)} \notag \\\end{align} \tag{19}\]
式\((16)\)和\((19)\)中\(\beta_1\)和\(\beta_2\)的分母是保持一致的,将求得的\(\beta_1\)和\(\beta_2\)带入式\((9)\)可以求得\(\beta_0\):
\[\beta_0 = \frac{1}{n}\sum_{i=0}^{n}{y_i}- \frac{1}{n}\beta_1\sum_{i=0}^{n}{t_i} - \frac{1}{n}\beta_2\sum_{i=0}^{n}{t_i^2} \\= \frac{1}{n}S_{y}- \frac{1}{n}\beta_1S_{t} - \frac{1}{n}\beta_2S_{t^2}\tag{20}\]
上述最小二乘法的消元法求解过程也是Android的VelocityTracker.cpp中使用的方法。
最小二乘法求解触摸事件的速度
随着时间的推移,过时的触摸事件点已经对当前速度计算的贡献几乎为0,因此只采用最近的20个触摸事件点,\(x\)和\(y\)两个方向分别进行计算,同时由于时间值精确到毫秒(甚至纳秒),那么使用上述方式计算可能会数值溢出,因此采用将触摸事件点的时间减去最新点的时间。
在计算触摸事件的速度之前,先将触摸点数据提前采集下来。可以使用MotionEventWriter进行采集,数据格式为:\(x,y,time\),如:- 533.0,471.0,5814487,533.0,471.0,5814496,532.0,472.0,5814506,531.71063,472.28937,5814509,531.0,473.0,5814515,527.8412,476.7906,5814523,526.0,479.0,5814527,517.0,490.0,5814537,514.4475,493.1197,5814539,505.0,504.0,5814546,490.0,522.0,5814556,489.4248,522.69025,5814556,472.0,546.0,5814565,461.23355,559.93304,5814573,455.0,568.0,5814577,429.0,602.0,5814587,421.55008,611.7422,5814589,402.0,640.0,5814596,376.0,677.0,5814606,375.41675,677.83,5814606,349.0,715.0,5814615,334.97095,736.6281,5814622,325.0,752.0,5814627,302.0,791.0,5814637,296.88904,799.6664,5814639,280.0,827.0,5814646,258.86536,862.5446,5814655,258.0,864.0,5814656,242.0,897.0,5814665,234.13586,912.7283,5814672,228.0,925.0,5814677,219.0,949.0,5814686,217.04567,954.21155,5814688,214.0,967.0,5814696,214.0,980.3627,5814705,214.0,981.0,5814706,218.0,988.0,5814715,223.07028,988.56335,5814722,227.0,989.0,5814727,242.0,983.0,5814736,245.16205,981.73517,5814738,263.0,971.0,5814746,286.52478,955.0032,5814755,288.0,954.0,5814756,317.0,931.0,5814765,335.05908,916.89136,5814772,349.0,906.0,5814777,385.0,875.0,5814786,392.34656,868.6738,5814788,423.0,844.0,5814796,456.2187,816.47595,5814805,458.0,815.0,5814806,488.0,792.0,5814815,503.0,780.5,5814820,518.0,768.0,5814828,544.0,751.0,5814836,549.912,747.13446,5814838,564.0,741.0,5814846,578.31866,737.1817,5814855,579.0,737.0,5814856,584.0,743.0,5814865,583.43176,749.25073,5814872,583.0,754.0,5814877,575.0,776.0,5814886,573.2179,780.9007,5814889,564.0,801.0,5814896,546.5539,833.9538,5814905,546.0,835.0,5814906,525.0,873.0,5814915,510.8347,896.6089,5814922,501.0,913.0,5814927,476.0,957.0,5814937,470.13397,967.3242,5814939,450.0,1001.0,5814946,425.18634,1041.6943,5814955,425.0,1042.0,5814955,406.0,1076.0,5814965,396.41208,1094.5767,5814972,390.0,1107.0,5814977,374.0,1141.0,5814986,370.01813,1149.4615,5814989,362.0,1170.0,5814996,354.00723,1192.9791,5815005,354.0,1193.0,5815005,352.0,1207.0,5815015,353.19043,1212.9521,5815022,354.0,1217.0,5815027,363.0,1221.0,5815036,365.1823,1221.97,5815039,376.0,1221.0,5815046,389.87677,1216.044,5815055,390.0,1216.0,5815055,413.0,1203.0,5815065,430.8009,1191.1327,5815072,443.0,1183.0,5815077,484.0,1153.0,5815086,493.81314,1145.8197,5815088,533.0,1115.0,5815096,583.2924,1073.5828,5815105,584.0,1073.0,5815105,631.0,1035.0,5815115,659.047,1012.79614,5815122,679.0,997.0,5815127,732.0,958.0,5815136,744.9325,948.48364,5815138,956.0,811.0,5815146,956.0,811.0,5815156
- import sys
- import matplotlib.pyplot as plt
- import numpy as np
- def load_points_from_file(filepath):
- data = np.loadtxt(filepath, delimiter=',').reshape(-1, 3)
- return data
- filepath = "pointer_data_20250817_100135.txt"
- if len(sys.argv) > 1:
- filepath = sys.argv[1]
- points = load_points_from_file(filepath)
- x = points[:, 0]
- y = points[:, 1]
- plt.scatter(x, y, c='r', marker='o')
- plt.xlabel("x")
- plt.ylabel("y")
- plt.show()
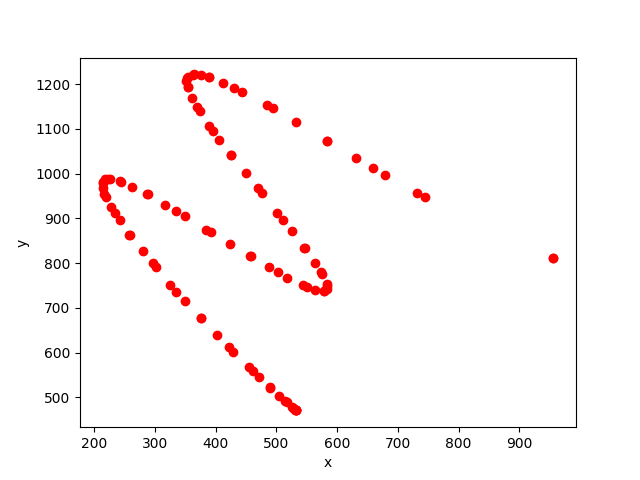
参照AndroidVelocityTracker.cpp的实现,根据公式\((16)\) \((19)\) \((20)\)分别对\(x\)和\(y\)计算恒加速运动模型参数:- import sys
- import matplotlib.pyplot as plt
- import numpy as np
- def solve_least_squares_deg2(y, t):
- Sy = 0.0
- St = 0.0
- St2 = 0.0
- St3 = 0.0
- St4 = 0.0
- Syt = 0.0
- Syt2 = 0.0
- for i in range(y.shape[0]):
- ti = t[i]
- yi = y[i]
- t2 = ti * ti
- t3 = t2 * ti
- t4 = t3 * ti
- Sy += yi
- St += ti
- St2 += t2
- St3 += t3
- St4 += t4
- Syt += yi * ti
- Syt2 += yi * t2
- n = len(y)
- denominator = (St * St2 / n - St3) * (St * St2 / n - St3) - (St2 * St2 / n - St4) * (St * St / n - St2)
- if denominator == 0:
- return None
- b2 = ((Sy * St / n - Syt) * (St * St2 / n - St3) - (Sy * St2 / n - Syt2) * (St * St / n - St2)) / denominator
- b1 = ((Sy * St2 / n - Syt2) * (St * St2 / n - St3) - (Sy * St / n - Syt) * (St2 * St2 / n - St4)) / denominator
- b0 = Sy / n - b1 * St / n - b2 * St2 / n
- return np.array([b0, b1, b2])
- def velocity_estimate(x, y, t):
- n = len(x)
- res_x = np.array([])
- res_y = np.array([])
- for i in range(n):
- s = 0
- if i > 20:
- s = i - 20
- e = i + 1
- sx = x[s:e].copy()
- sy = y[s:e].copy()
- st = t[s:e].copy()
- for j in range(len(st)):
- st[j] = st[j] - t[i]
- param_y = solve_least_squares_deg2(sy, st)
- param_x = solve_least_squares_deg2(sx, st)
- if param_y is not None:
- res_y = np.append(res_y, param_y[1])
- else:
- res_y = np.append(res_y, 0)
- if param_x is not None:
- res_x = np.append(res_x, param_x[1])
- else:
- res_x = np.append(res_x, 0)
- return res_x, res_y
- def load_points_from_file(filepath):
- data = np.loadtxt(filepath, delimiter=',').reshape(-1, 3)
- return data
- filepath = "pointer_data_20250817_100135.txt"
- if len(sys.argv) > 1:
- filepath = sys.argv[1]
- points = load_points_from_file(filepath)
- x = points[:, 0]
- y = points[:, 1]
- t = points[:, 2]
- res = velocity_estimate(x, y, t)
- vx = res[0]
- vy = res[1]
- plt.figure(1)
- plt.scatter(x, y, c='r', marker='o')
- plt.xlabel("x")
- plt.ylabel("y")
- plt.figure(2)
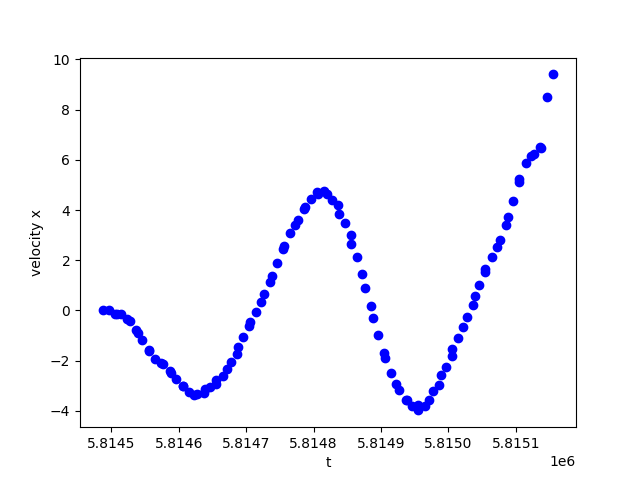
- plt.scatter(t, vx, c='b', marker='o')
- plt.xlabel("t")
- plt.ylabel("velocity x")
- plt.figure(3)
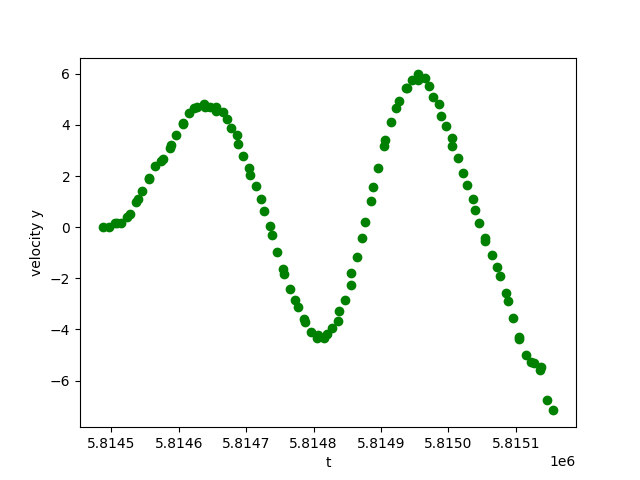
- plt.scatter(t, vy, c='g', marker='o')
- plt.xlabel("t")
- plt.ylabel("velocity y")
- plt.show()
参考
[1] VelocityTracker.cpp
[2] 最小二乘法_百度百科
[3] MotionEvent
来源:程序园用户自行投稿发布,如果侵权,请联系站长删除
免责声明:如果侵犯了您的权益,请联系站长,我们会及时删除侵权内容,谢谢合作! |