卡尔曼滤波算法原理概述

  卡尔曼滤波（Kalman Filter）是一种高效的递归数学算法，用于从包含噪声的观测数据中动态估计系统的状态。它广泛应用于信号处理、导航、控制系统、机器人等领域。其核心思想是通过结合预测（系统模型）和更新（观测数据）来最小化估计误差的协方差。
一、状态空间模型

  系统由 “状态方程” 和 “观测方程” 描述。
1. 状态方程（预测模型）


\[x_k=F_kx_{k-1+B_ku_k+w_k}\]
其中，
   \(x_k\)：当前时刻的状态向量（需估计的量）。
   \(F_k\)：状态转移矩阵（描述系统如何从\(x_{k-1}\) 演化到\(x_k\)）。
   \(u_k\)：控制输入（可选）。
   \(w_k\)：过程噪声（假设为高斯白噪声，协方差为\(Q_k\)）。
2. 观测方程（测量模型）


\[z_k=H_kx_k+v_k\]
其中，
  \(z_k\)：观测向量。
  \(H_k\)：观测矩阵（将状态映射到观测空间）。
  \(v_k\)：观测噪声（高斯白噪声，协方差为\(R_k\)）。
二、算法的两步过程：预测与更新

  卡尔曼滤波通过预测和更新交替进行。
1. 预测（时间更新）

  状态预测：根据上一时刻状态估计值，预测当前状态

\[\hat x_{k}^{-}=F_k\hat x_{k-1}+B_ku_k\]
  误差协方差预测：更新预测状态的不确定性

\[P_k^{-}=F_kP_{k-1}F_k^T+Q_k\]
  其中，\(P_k^{-}\)是先验误差协方差矩阵，表示预测的不确定性；\(Q_k\)为过程噪声协方差。
2. 更新（测量更新）

结合观测数据修正预测值：
(1)计算卡尔曼增益\(K_k\)（权衡预测与观测的权重）

\[K_k=P_k^{-}H_k^T(H_kP_k^{-}H_k^T+R_k)^{-1}\]
  （注：\(K_k\)的值反映观测值对状态估计的修正程度：噪声越大，增益越小）
(2) 更新状态估计（结合预测值与观测值，得到最优估计）

\[\hat x_k=\hat x_k^{-}+K_k(z_k-H_k\hat x_k^{-})\]
  其中，\(z_k-H_k\hat x_k^{-}\)为观测残差，体现预测与实际观测的偏差。
(3) 更新误差协方差（更新当前状态估计的不确定性）

\[P_k=(I-K_kH_k)P_k^{-}\]
  其中，\(I\)为单位矩阵，更新后协方差矩阵反映估计精度的提升。
  卡尔曼增益\(K_k\)的设计使得后验误差协方差\(P_k\)最小化，即估计值是最小均方误差（MMSE）意义下的最优估计。
三、关键假设

  a. 线性系统模型（非线性需扩展卡尔曼滤波EKF或无迹卡尔曼滤波UKF）。
  b. 过程噪声和观测噪声为高斯分布且互不相关。
  c. 初始状态和协方差已知。
四、直观类比：以温度估计为例

  预测阶段：根据昨日温度和天气模型，预测今日温度为 25℃，并知道该预测的误差范围（如 ±3℃）。
  观测阶段：温度计显示 26℃，但已知温度计误差为 ±1℃。
  卡尔曼滤波处理：
    计算增益：考虑预测误差（3℃）和观测误差（1℃），增益更偏向观测值（如 0.75）；
    状态更新：最终估计温度 = 25 + 0.75×(26-25)=25.75℃，误差范围缩小（如 ±0.5℃）。
五、Python示例

1. import matplotlib
2. matplotlib.use('TkAgg')
4. import numpy as np
5. import matplotlib.pyplot as plt
7. plt.rcParams['font.sans-serif']=['SimHei']  # 中文支持
8. plt.rcParams['axes.unicode_minus']=False  # 负号显示
10. def kalman_filter(data, initial_state, initial_covariance, process_variance, measurement_variance):
11.     """
12.     参数:
13.     data: 观测数据数组
14.     initial_state: 初始状态估计
15.     initial_covariance: 初始状态协方差
16.     process_variance: 过程噪声方差
17.     measurement_variance: 测量噪声方差
19.     返回:
20.     滤波后的状态估计数组
21.     """
22.     n = len(data)
23.     state_estimates = np.zeros(n)
24.     state_covariances = np.zeros(n)
26.     # 初始化
27.     state_estimates[0] = initial_state
28.     state_covariances[0] = initial_covariance
30.     for i in range(1, n):
31.         # 预测步骤
32.         predicted_state = state_estimates[i - 1]  # 假设状态转移为恒等变换
33.         predicted_covariance = state_covariances[i - 1] + process_variance
35.         # 更新步骤
36.         kalman_gain = predicted_covariance / (predicted_covariance + measurement_variance)
37.         state_estimates[i] = predicted_state + kalman_gain * (data[i] - predicted_state)
38.         state_covariances[i] = (1 - kalman_gain) * predicted_covariance
40.     return state_estimates
42. # 生成模拟数据
43. np.random.seed(42)
44. true_values = np.linspace(0, 10, 100)  # 真实信号
45. measurements = true_values + np.random.normal(0, 1, 100)  # 带噪声的观测
47. # 应用卡尔曼滤波
48. filtered = kalman_filter(
49.     data=measurements,
50.     initial_state=0,
51.     initial_covariance=1,
52.     process_variance=0.01,
53.     measurement_variance=1
54. )
56. # 绘制结果
57. plt.figure(figsize=(10, 6))
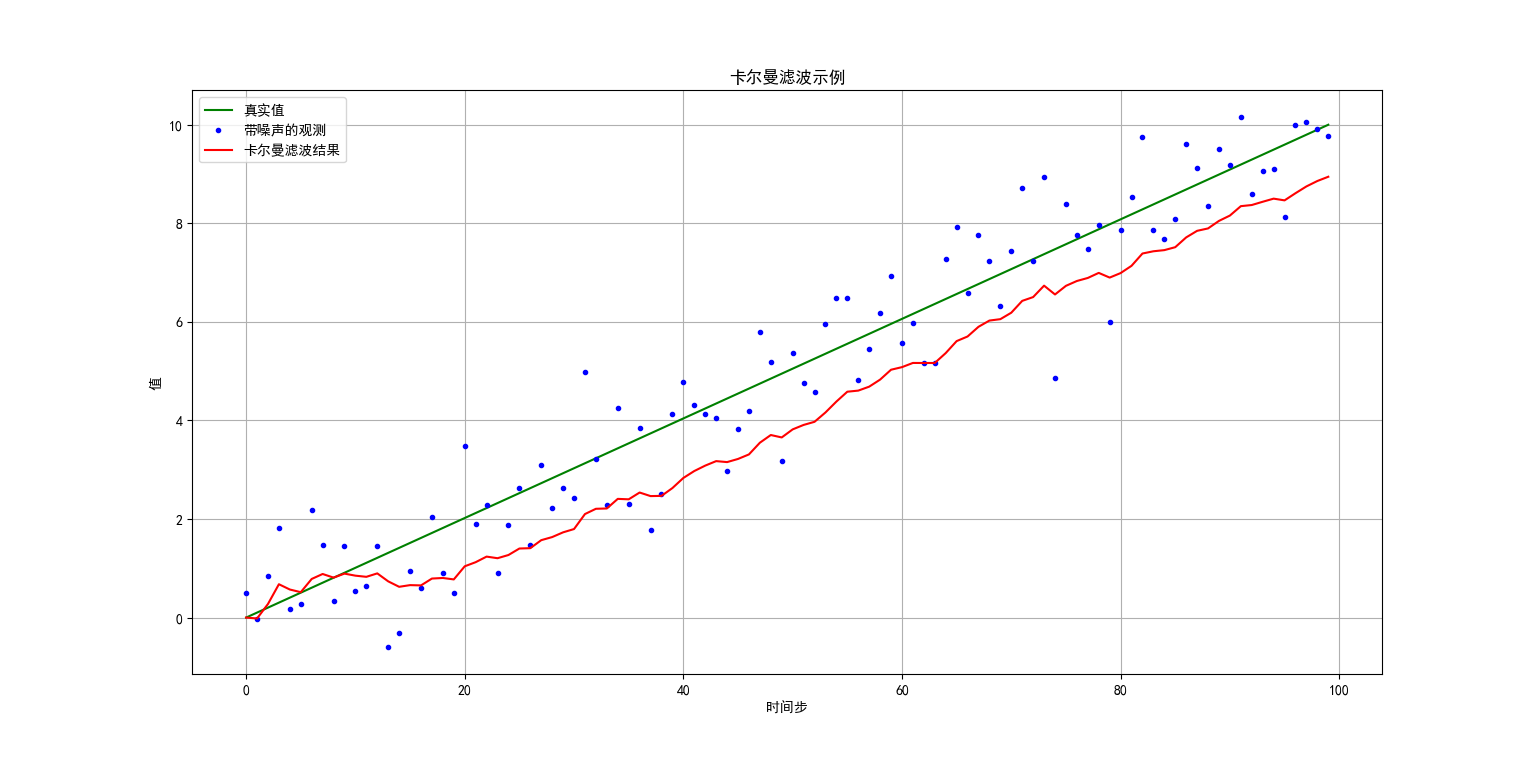
58. plt.plot(true_values, 'g-', label='真实值')
59. plt.plot(measurements, 'b.', label='带噪声的观测')
60. plt.plot(filtered, 'r-', label='卡尔曼滤波结果')
61. plt.legend()
62. plt.title('卡尔曼滤波示例')
63. plt.xlabel('时间步')
64. plt.ylabel('值')
65. plt.grid(True)
66. plt.show()

复制代码

End.

来源：程序园用户自行投稿发布，如果侵权，请联系站长删除
免责声明：如果侵犯了您的权益，请联系站长，我们会及时删除侵权内容，谢谢合作！